Mohr's Circle
Introduced by Otto Mohr in 1882, Mohr's Circle illustrates principal stresses and stress transformations via a graphical format,
The two principal stresses are shown in red, and the maximum shear stress is shown in orange. Recall that the normal stresses equal the principal stresses when the stress element is aligned with the principal directions, and the shear stress equals the maximum shear stress when the stress element is rotated 45° away from the principal directions.
As the stress element is rotated away from the principal (or maximum shear) directions, the normal and shear stress components will always lie on Mohr's Circle.
Mohr's Circle was the leading tool used to visualize relationships between normal and shear stresses, and to estimate the maximum stresses, before hand-held calculators became popular. Even today, Mohr's Circle is still widely used by engineers all over the world.
Derivation of Mohr's Circle:
To establish Mohr's Circle, we first recall the stress transformation formulas for plane stress at a given location,
Using a basic trigonometric relation (cos22q + sin22q = 1) to combine the two above equations we have,
This is the equation of a circle, plotted on a graph where the abscissa is the normal stress and the ordinate is the shear stress. This is easier to see if we interpret sx and sy as being the two principal stresses, and txy as being the maximum shear stress. Then we can define the average stress, savg, and a "radius" R (which is just equal to the maximum shear stress),
The circle equation above now takes on a more familiar form,
The circle is centered at the average stress value, and has a radius R equal to the maximum shear stress, as shown in the figure below,

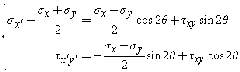









No comments:
Post a Comment